4.5 Constraints

The same structure can be represented in an infinite number of coordinate systems (“modular invariance”). Many of these equivalent choices will lead to very flat unit cells, which creates problems for structure relaxation and energy calculation (e.g., a very large number of 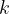$k$ -points are needed). The constraint, well known in crystallography, that the cell angles be between 60 $^\circ$ and 120 $^\circ$ , does not remove all redundancies and problematic cells (e.g., thus allowed cells with 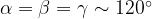$\alpha =\beta =\gamma \sim 120^\circ$ are practically flat). Therefore, we developed ^{21; 24} a scheme to obtain special cell shapes with the shortest cell vectors. 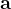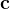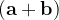This transformation can be performed if there is at least one lattice vector whose projection onto any other cell vector or the diagonal vector of the opposite cell face is greater (by modulus) than half the length of that vector, i.e., for pairs $\textbf{a}$ and $\textbf{b}$ , or $\textbf{c}$ and $(\textbf{a}+\textbf{b})$ these criteria are:

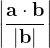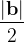$\displaystyle \label{eq:cellCons} \left\|\frac{\bf a \cdot b}{\bf \vert b \vert }\right\|$	$\displaystyle >$	$\displaystyle \frac{\bf \|b\|}{2} \label{eq:cellCons1}$	(2)
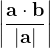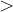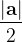$\displaystyle \left\|\frac{\bf a \cdot b}{\bf \vert a \vert }\right\|$	$\displaystyle >$	$\displaystyle \frac{\bf \|a\|}{2} \label{eq:cellCons2}$	(3)
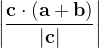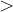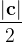$\displaystyle \left\|\frac{\bf c \cdot (a + b)}{\bf \vert c \vert }\right\|$	$\displaystyle >$	$\displaystyle \frac{\bf \|c\|}{2} \label{eq:cellCons3}$	(4)
$\displaystyle \left\|\frac{\bf c \cdot (a + b)}{\bf \vert a+b \vert }\right\|$	$\displaystyle >$	$\displaystyle \frac{\bf \|a+b\|}{2} \label{eq:cellCons4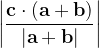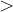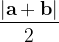}$	(5)

For instance, for the criterion 2 the new vector 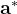$\bf a^*$ equals:

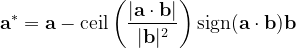$\begin{equation} {\bf a}^* = {\bf a} - {\rm ceil} \left( \frac{\vert {\bf a} \cdot {\bf b} \vert }{\vert {\bf b} \vert ^2} \right){\rm sign}({\bf a}\cdot {\bf b}){\bf b} \end{equation}$

(6)

This transformation is performed iteratively, completely avoids pathological cell shapes, and thus solves the problem. During this transformation, the atomic fractional coordinates are transformed so that the original and transformed structures are identical (during the transformation, the Cartesian coordinates of the atoms remain invariant).

$\triangleright$ variable blue minVectorLength

Meaning: Sets the minimum length of a cell parameter of a newly generated structure.

Default: 1.8 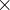covalent diameter of the largest atom. For molecular crystals (calculationType = 310, 311) default value is 1.8 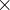max(MolCenters).

Format:

2.0 : minVectorLength

Commonly used computational methods (pseudopotentials, PAW, LAPW, and many parametric forcefields) fail when the interatomic distances are too small. This situation needs to be avoided by specifying the minimum distances between each pair of atoms using the IonDistances square matrix:

$\triangleright$ variable blue IonDistances

Meaning: Sets the minimum interatomic distance matrix between different atom types. Structures with distances lower than IonDistances will be strictly discarded.

Default: the IonDistances between atom A and B are estimated as 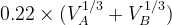but not larger than 1.2 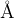, and 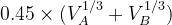in molecular calculations, where 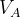and 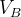are the default volumes of atom A and B estimated in USPEX.

Format:

% IonDistances 1.0 1.0 0.8 1.0 1.0 0.8 0.8 0.8 1.0 % EndDistances

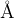NOTE: The dimensions of this matrix must be equal to the number of atomic species. If the compound in the example above is MgSiO $_3$ , the matrix reads as follows: the minimum Mg–Mg distance allowed in a newly generated structure is 1.0 $\text {\r{A}}$ , the minimum Mg–Si, Si–Si and O–O distances are also 1.0 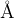$\text {\r{A}}$ , and the minimum Mg–O and Si–O distances are 0.8 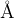$\text {\r{A}}$ . You can use this keymatrix to incorporate further system-specific information: e.g., if you know that Mg atoms prefer to be very far apart and are never closer than 3 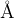$\text {\r{A}}$ in your system, you can specify this information. Beware, however, that the larger these minimum distances, the more difficult it is to generate structures fulfilling these constraints (especially for large systems), so strive for a compromise and remember that IonDistances must be much smaller than the actual distances in the crystal: realistic distances will be achieved by structure relaxation. What IonDistances trick does is to avoid structures which cannot be relaxed correctly.

$\triangleright$ variable blue constraint_enhancement

Meaning: Allows one to apply the stricter constraints of the IonDistances matrix (by constraint_enhancement times) for symmetric random structures (for all variation operators, unenhanced IonDistances matrix still applies). Only use it if you know what you are doing.

Default: 1

Format:

1 : constraint_enhancement

For molecular crystals, the following keyblock is extremely important:

$\triangleright$ variable blue MolCenters

Meaning: Matrix of minimal distances between the geometric centers of molecules. Any distances lower than these indicate large overlap of the molecules, are unphysical and will be strictly avoided.

Default: none.

Format:

% MolCenters 5.5 7.7 0.0 9.7 % EndMol

NOTE: In the above example, there are two types of molecules. In all of the generated structures, the distance between the geometric centers of the molecules of the first type must be at least 5.5 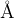$\text {\r{A}}$ (A–A distance), the distance between the centers of the molecules of the first and second type — 7.7 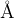$\text {\r{A}}$ (A–B distance), and the distance between the molecules of the second type — 9.7 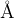$\text {\r{A}}$ (B–B distance).