| USPEX 10.5 manual |
 variable calculationMethod
variable calculationMethod
Meaning: Specifies the method of calculation
Possible values (characters):
USPEX — evolutionary algorithm for crystal structure prediction
META — evolutionary metadynamics
VCNEB — transition path determination using the variable-cell nudged elastic band method
PSO — corrected PSO algorithm
TPS — transition path sampling method
MINHOP — minima hopping method
COPEX — coevolutionary technique for reliable variable-composition ternary runs
Default: USPEX
Format:
USPEX : calculationMethod
 variable calculationType
variable calculationType
Meaning: Specifies type of calculation, i.e., whether the structure of a bulk crystal, nanoparticle, or surface is to be predicted. This variable consists of three indices: dimensionality, molecularity and compositional variability, and the spin option with character “s” or “S”:
dimensionality:
“3” — bulk crystals
“2” — surfaces, “–2” — 2D-crystals
“1” — polymers
“0” — nanoparticles
molecularity:
“0” — non-molecular
“1” — molecular calculations
variability of chemical composition in the calculation:
“0” — fixed composition
“1” — variable composition
magnetic calculation :
“s” or “S” – enable the magnetic calculation
Default: 300
Format:
301 : calculationType
NOTE: If calculationType=310, i.e., a prediction for a molecular crystal is to be performed, then USPEX expects you to provide files MOL_1, MOL_2, …with molecular geometries for all types of molecules, and these molecules will be placed in the newly generated structures as whole objects. Available options: 300 (s300), 301 (s301), 310, 311, 000 (s000), 200 (s200), 201 (s201), –200 (–s200), –201 (–s201), 110.
 variable optType
variable optType
Meaning: This keyblock specifies the property (or properties) that you want to optimize. Default is minimization for enthalpy (and finite-temperature free energy) and volume, and maximization for the rest of optType — but you can explicitly specify whether you want minimization or maximization. You can also optimize properties to the target value (e.g., band gaps close to 1.34 eV are interesting for photovoltaics).
Possible values (characters):
Name |
Number |
Description |
enthalpy |
1 |
to find the stable phases |
volume |
2 |
minimization of volume per atom |
(to find the densest structure) |
||
hardness |
3 |
hardness maximization |
(to find the hardest phase) |
||
struc_order |
4 |
maximization of the degree of order |
(to find the most ordered structure) |
||
density |
5 |
maximization of density |
diel_sus |
6 |
maximization of the static dielectric susceptibility |
(only for VASP and GULP) |
||
bandgap |
7 |
maximization of the band gap |
(only for VASP) |
||
diel_gap |
8 |
maximization of electrical energy storage capacity |
(only for VASP) |
||
mag_moment |
9 |
maximization of the magnetization (i.e. magnetic moment per volume) |
(only for VASP) |
||
quasientropy |
10 |
maximization of structural quasientropy |
birefringence |
11 |
difference between largest and smallest eigenvalues of |
the refractive index tensor (only for VASP) |
||
HalfMetalicity |
12 |
maximization halfmetalicity parameter (only for VASP) |
ZT |
14 |
thermoelectric figure of merit ZT |
(only for VASP and BoltzTraP) |
||
Fphon |
17 |
free energy at finite temperature |
Elasticity-related properties (”11**”):
Value |
Number |
Description |
K, Bulk Modulus |
1101 |
maximization of bulk modulus |
G, Shear Modulus |
1102 |
maximization of shear modulus |
E, Young’s Modulus |
1103 |
maximization of Young’s modulus |
v, Poisson’s ratio |
1104 |
maximization of Poisson’s ratio |
G/K, Pugh’s modulus ratio |
1105 |
maximization of Pugh’s modulus ratio |
Hv, Vickers hardness |
1106 |
maximization of Vickers hardness |
Kg, Fracture toughness |
1107 |
maximization of fracture toughness |
D, Debye temperature |
1108 |
maximization of Debye temperature |
Vm, sound velocity |
1109 |
maximization of sound velocity |
S-wave velocity |
1110 |
maximization of S-wave velocity |
P-wave velocity |
1111 |
maximization of P-wave velocity |
NOTE: Calculation of these elasticity-related properties are supported only for VASP (starting from VASP 5.1) and GULP. For VASP users, you need to add one more INCAR_* file to the Specific/ folder with the parameters IBRION=6, ISIF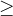 3 and NFREE=4. The estimates of bulk, shear and Young’s moduli are the Voigh-Reuss-Hill (VRH) averages. Note that such calculations of the elastic properties may be numerically unstable and you will need to check the results carefully. Or use another, numerically very robust, way for calculating elastic moduli - using machine learning, see below.
3 and NFREE=4. The estimates of bulk, shear and Young’s moduli are the Voigh-Reuss-Hill (VRH) averages. Note that such calculations of the elastic properties may be numerically unstable and you will need to check the results carefully. Or use another, numerically very robust, way for calculating elastic moduli - using machine learning, see below.
Users also can perform the calculation of the elastic properties using Machine Learing (ML) approach, where the elastic moduli are computed using a graph convolutional neural network 19 and then hardness and fracture toughness are evaluated are calculated with the Mazhnik-Oganov model 20.
ML-based elasticity-related properties (”12**”):
Value |
Number |
Description |
K, Bulk Modulus |
1201 |
maximization of bulk modulus |
G, Shear Modulus |
1202 |
maximization of shear modulus |
E, Young’s Modulus |
1203 |
maximization of Young’s modulus |
v, Poisson’s ratio |
1204 |
maximization of Poisson’s ratio |
G/K, Pugh’s modulus ratio |
1205 |
maximization of Pugh’s modulus ratio |
Hv, Vickers hardness |
1206 |
maximization of Vickers hardness |
Kg, Fracture toughness |
1207 |
maximization of fracture toughness |
NOTE: the implemented formula for fracture toughness works only for insulating materials (and carbides, borides, hydrides)
Default: enthalpy
Format:
% optType
enthalpy (equivalent to Min_enthalpy)
% EndOptType
another example:
% optType
Min_(bandgap-1.34)^2
% EndOptType
NOTE: In the latter case, we optimize a mathematical expression as the optType variable. The mathematical expression should be in parentheses and should be a valid MATLAB expression. The whole expression (including min_ and max_ if applicable) should be one unit, do NOT put blank space between the expression compartments. For example “( bandgap - 1.3 ) ^2"or min_ (bandgap-3) are NOT valid formats.
Multiobjective (Pareto) optimizations are also available by specifying several fitnesses in the optType keyblock, e.g.,
% optType
3 1
% EndOptType
or
% optType
max_Hardness enthalpy
% EndOptType
In multiobjective optimization, it is useful to start with a few generations of enthalpy-only optimization and then switch to Pareto optimization of all desired properties. The number of initial generations spent on enthalpy-only optimization by default is zero and is given in brackets as follows:
% optType
3 6 [5]
% EndOptType
or
% optType
max_Hardness min_Diel_sus [5]
% EndOptType
This means USPEX does enthalpy-only optimization up to the 5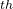 generation, and then switches to multiobjective optimization.
generation, and then switches to multiobjective optimization.
Fig. 5a gives an example of hardness maximization for TiO (optType=hardness), showing maximum possible hardness 14 GPa21 and refuting claims of Dubrovinsky (2001) about ultrahardness of TiO
(optType=hardness), showing maximum possible hardness 14 GPa21 and refuting claims of Dubrovinsky (2001) about ultrahardness of TiO 22, a good example of how a simple USPEX run can resolve a long-standing dispute. Fig. 5b shows an example of Pareto optimization, clearly displaying frequent trade-off between stability and properties.
22, a good example of how a simple USPEX run can resolve a long-standing dispute. Fig. 5b shows an example of Pareto optimization, clearly displaying frequent trade-off between stability and properties.
![\includegraphics[scale=0.75]{pic/hardness.png}](images/img-0040.png)
Notes: If optType=bandgap or diel_gap, instead of the gap we use an extended function that also behaves continuously for metals — namely, 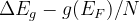 , where
, where 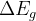 is the gap,
is the gap, 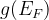 is the density of states at the Fermi level (for metals) and
is the density of states at the Fermi level (for metals) and 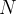 is the number of atoms in the unit cell. Thanks to the continuity of this function, global maximization of gap-related quantities can even be performed for metallic solutions. For metals it is equal to the DOS at the Fermi level, for semiconductors and insulators — to the band gap.
is the number of atoms in the unit cell. Thanks to the continuity of this function, global maximization of gap-related quantities can even be performed for metallic solutions. For metals it is equal to the DOS at the Fermi level, for semiconductors and insulators — to the band gap.
![\includegraphics[scale=0.18]{pic/hardness_example.png}](images/img-0044.png)
 .
.  variable atomType
variable atomType
Meaning: Describes the identity of each type of atom.
Default: none, must specify explicitly
Format:
If you prefer to use the atomic numbers from Mendeleev’s Periodic Table of the Elements, specify:
% atomTypeOr, if you prefer to use atomic names, specify:
% atomType
Mg Si O
% EndAtomType
You can alternatively specify the full names of the elements, for example:
% atomType
Magnesium Silicon Oxygen
% EndAtomType
 variable numSpecies
variable numSpecies
Meaning: Specifies the number of atoms of each type.
Default: none, must specify explicitly
Format:
% numSpecies
4 4 12
% EndNumSpecies
This means there are 4 atoms of the first type, 4 of the second type, and 12 of the third type.
Notes: For variable-composition calculations, you have to specify the compositional building blocks as follows:
% numSpecies
2 0 3
0 1 1
% EndNumSpecies
This means that the first building block has formula A C
C and the second building block has formula BC, where A, B and C are described in the block atomType. All structures will then have the formula
and the second building block has formula BC, where A, B and C are described in the block atomType. All structures will then have the formula 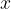 A
A C
C +
+ 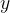 BC with
BC with 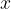 ,
, 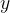 = (0,1,2,…) — or A
= (0,1,2,…) — or A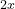 B
B C
C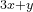 . If you want to do prediction of all possible compositions in the A-B-C system, you should specify:
. If you want to do prediction of all possible compositions in the A-B-C system, you should specify:
% numSpecies
1 0 0
0 1 0
0 0 1
% EndNumSpecies
You can also do fixed-composition calculations with a variable number of formula units; in this case set calculationType=300, the composition of one formula unit, for example, A BC
BC :
:
% numSpecies
2 1 4
% EndNumSpecies
14 : minAt
28 : maxAt
 variable magRatio
variable magRatio
Meaning: Initial ratio of structures with different magnetic orders, namely NM, FM-LS, FM-HS, AFM-L, AFM-H, FM-LH, AF-LH states, respectively. Only VASP is supported.
Default: 0.1, 0.9/4, 0.9/4, 0.9/4, 0.9/4, 0, 0
Format:
% magRatio
1/8 1/8 1/8 1/8 1/8 0 0
% EndMagRatio
This means that probabilities of generating NM, FM-LS, FM-HS, AFM-L, AFM-H structures are all 20% (NOT 1/8 here! The number are rescaled so that sum of probabilities is 1.). No structures with FM-LH, AF-LH magnetic states will be generated.
Notes:
(1) The sum of magRatio can be larger than 1, the ratio will be rescaled to 1 automatically.
(2) The meaning and initial magnetic moment value in USPEX:
NM — non-magnetic;
FM-LS — low-spin ferromagnetic;
FM-HS — high-spin ferromagnetic;
AFM-L — low-spin antiferromagnetic;
AFM-H — high-spin antiferromagnetic;
FM-LH — low/high spin mixed ferromagnetic;
AF-LH — low/high spin mixed antiferromagnetic.
(3) For NM states, the initial magnetic moment will be 0 for all atoms. The initial magnetic moment MAGMOM of the atoms will be set to 1 and 4 for low and high spin states, respectively. For low/high spin mixed states, MAGMOM will be set to 1 or 4 randomly for each atom.
(4) AFM type structures will not be generated when having odd number of magnetic atoms in a unit cell.
(5) magRatio is also used for the mutation ratio in spinmuation operation.
 variable ldaU
variable ldaU
Meaning: Specifies Hubbard U value for atoms of each type with the LDA+U method. Only VASP is supported.
Default: 0 for each type of atoms
Format:
% ldaU
4 0
% EndLdaU
 variable ExternalPressure
variable ExternalPressure
Meaning: Specifies external pressure at which you want to find structures, in GPa.
Default: 0
Format:
100 : ExternalPressure
NOTE: As of USPEX version 9.4.1 pressure value (in GPa) is set by the tag ExternalPressure in the INPUT.txt file. Please: do not specify it in relaxation files in the Specific/ folder.
 variable valences
variable valences
Meaning: Describes the valences of each type of atom. Used only to evaluate bond hardnesses, which are used for computing the approximate dynamical matrix (for softmutation) and hardness of the crystal.
Default: USPEX has a table of default valences (see Appendix 9.9). Beware, however, that for some elements (e.g., N, S, W, Fe, Cr, etc.) many valence states are possible. Unless you calculate hardness, just use the default values by not specifying valences. If you do calculate the hardness, you need to carefully and explicitly specify the valence.
Format:
% valences
2 4 2
% EndValences
 variable goodBonds
variable goodBonds
Meaning: Specifes, in the matrix form, the minimum bond valences for contacts that will be considered as important bonds. Like the IonDistances matrix (see below), this is a square matrix. This is only used in calculations of hardness and in softmutation. One can estimate these values for a given bond type taking goodBonds=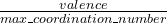 or slightly smaller.
or slightly smaller.
Default: USPEX can make a reasonable default estimation of goodBonds, you will see the values in OUTPUT.txt file. This should be sufficient for most purposes, but for hardness calculations you may need to carefully examine these values and perhaps set them manually. For more details, see Appendix 9.10
Format:
% goodBonds
10.0 10.0 0.2
10.0 10.0 0.5
0.2 0.5 10.0
% EndGoodBonds
Notes: The dimensionality of this matrix must be equal to either the number of atomic species or unity. If only one number is used, the matrix is filled with this number. The above matrix reads as follows: to be considered a bond, the Mg–Mg distance should be short enough to have bond valence of 10 or more, the same for Mg–Si, Si–Si, and O–O bonds (by using such exclusive criteria, we effectively disregard these interactions from the softmutation and hardness calculations), whereas Mg–O bonds that will be considered for hardness and softmutation calculations will have a bond valence of 0.2 or more, and the Si–O bonds will have a bond valence of 0.5 or more.
 variable checkMolecules
variable checkMolecules
Meaning: Switches on/off post-relaxation check that original molecules (files MOL_1, MOL_2, …) are intact. Useful for molecular crystals (calculationType=310, 311).
Possible values (integer):
0 — check is not performed, structures with broken or merged molecules are considered. (We strongly suggest users not to use this.)
1 — check is performed, all the structures with broken or merged molecules are discarded.
Default: 1
Format:
1 : checkMolecules
 variable checkConnectivity
variable checkConnectivity
Meaning: Switches on/off hardness calculation and connectivity-related criteria in softmutation.
Possible values (integer):
0 — connectivity is not checked, no hardness calculations;
1 — connectivity is taken into account, hardness is calculated.
Default: 0
Format:
1 : checkConnectivity
 variable fitLimit
variable fitLimit
Meaning: USPEX stops when it finds a fitness value equal to or better than fitLimit
Default: no default, has to be specified by the user.
Format:
-9.319 : fitLimit