1. Features, aims and history of USPEX

1.1. Overview

USPEX stands for Universal Structure Predictor: Evolutionary Xtallography…and in Russian “uspekh” means “success”, which is appropriate given the high success rate and many useful results produced by this method! The USPEX code possesses many unique capabilities for computational materials discovery.

From the beginning in 2004, non-empirical crystal structure prediction was the main aim of the USPEX project. In addition to this, USPEX also allows one to predict a large set of robust metastable structures and perform several types of simulations using various degrees of prior knowledge. Starting from 2010, our code explosively expanded to other types of problems, and from 2012 includes many complementary methods.

The problem of crystal structure prediction is very old and does, in fact, constitute the central problem of theoretical crystal chemistry. In 1988 John Maddox 1 wrote that:

“One of the continuing scandals in the physical sciences is that it remains in general impossible to predict the structure of even the simplest crystalline solids from a knowledge of their chemical composition… Solids such as crystalline water (ice) are still thought to lie beyond mortals’ ken”.

It is immediately clear that the problem at hand is that of global optimization, i.e., finding the global minimum of the free energy of the crystal (per mole) with respect to variations of the structure. To get some feeling of the number of possible structures, let us consider a simplified case of a fixed cubic cell with volume \(V\), within which one has to position \(N\) identical atoms. For further simplification let us assume that atoms can only take discrete positions on the nodes of a grid with resolution \(\delta\). This discretization makes the number of combinations of atomic coordinates \(C\) finite:

(1.1.1)\[C=\frac{1}{(V/\delta^3)}\frac{(V/\delta^3)!}{[(V/\delta^3)-N]!N!}\]

If \(\delta\) is chosen to be a significant fraction of the characteristic bond length (e.g., \(\delta = 1 \text{Å} \) would be a reasonable estimate of the number of local minima of the free energy. If there are more than one type of atoms, the number of different structures significantly increases. Assuming a typical atomic volume \(\sim\) \(10 \text{Å}^3\), and taking into account Stirling’s formula (\(n!\approx\sqrt{2 \pi n}(n/e)^n\)), the number of possible structures for an element A (compound AB) is \(10^{11}\) (\(10^{14}\)) for a system with 10 atoms in the unit cell, \(10^{25}\) (\(10^{30}\)) for a system with 20 atoms in the cell, and \(10^{39}\) (\(10^{47}\)) for a system with 30 atoms in the unit cell. These numbers are enormous and practically impossible to deal with even for small systems with a total number of atoms \(N\sim10\). Even worse, complexity increases exponentially with \(N\). It is clear then, that point-by-point exploration of the free energy surface going through all possible structures is not feasible, except for the simplest systems with \(\sim\)1-5 atoms in the unit cell.

USPEX 2,3 employs an evolutionary algorithm devised by A.R. Oganov and C.W. Glass, with major subsequent contributions by A.O. Lyakhov, Q. Zhu, G.R. Qian, P. Bushlanov, Z. Allahyari, S. Lepeshkin and A. Samtsevich. Its efficiency draws from the carefully designed variation operators, while its reliability is largely due to the use of state-of-the-art ab initio simulations inside the evolutionary algorithm. The strength of evolutionary simulations is that they do not require any system-specific knowledge (except the chemical composition) and are self-improving, i.e. in subsequent generations increasingly good structures are found and used to generate new structures. This allows a “zooming in” on promising regions of the energy (or property) landscape (Fig. 1.1.1). Furthermore, by carefully designing variation operators, it is very easy to incorporate additional features into an evolutionary algorithm.

_images/energy_landscape.png

Fig. 1.1.1 2D projection of the reduced landscape of \(\text{Au}_8\text{Pd}_4\), showing clustering of low-energy structures in one region. The landscape was produced using the method of Oganov & Valle (2009).

A major motivation for the development of USPEX was the discovery of the post-perovskite phase of \(\text{MgSiO}_3 \)), which was made in 2004 4,5 and has significantly changed models of the Earth’s internal structure. In mid-2005 we had the first working version of USPEX. By September 2010, when USPEX was publicly released, the user community numbered nearly 200, over 800 users in May 2012, over 2100 in December 2014, and over 4500 in December 2018.

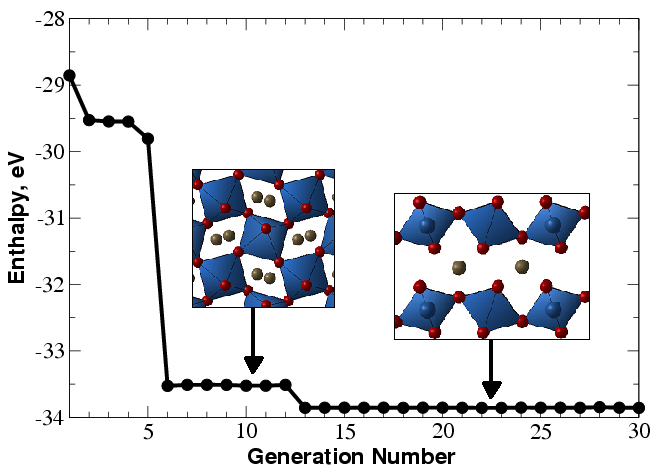
_images/prediction_of_the_crystal_structure_of_MgSiO3.png

Fig. 1.1.2 Prediction of the crystal structure of \(\text{MgSiO}_3\) at 120GPa (20 atoms/cell). Enthalpy of the best structure as a function of generation is shown. Between the 6\(^{th}\) and 12\(^{th}\) generations the best structure is perovskite, but at the 13\(^{th}\) generation the global minimum (post-perovskite) is found. This simulation was performed in 2005 using one of the first versions of USPEX combined with ab initio calculations. It used no experimental information and illustrates that USPEX can find both the stable and low-energy metastable structures in a single simulation. Each generation contains 30 structures. This figure illustrates the slowest of \(\sim\)10 calculations performed by the very first version of USPEX — and even that was pretty fast!

The popularity of USPEX is due to its extremely high efficiency and reliability. This was shown in the First Blind Test for Inorganic Crystal Structure Prediction 6, where USPEX outperformed the other methods it was tested against (simulated annealing and random sampling). Random sampling (a technique pioneered for structure prediction by Freeman and Schmidt in 1993 and 1996, respectively, and since 2006 revived by Pickard 7 under the name AIRSS) is the simplest, but also the least successful and computationally the most expensive strategy. Even for small systems, such as GaAs with 8 atoms/cell, these advantages are large (random sampling requires on average 500 structure relaxations to find the ground state in this case, while USPEX finds it after only \(\sim\) 30 relaxations! (Fig. 1.1.3)). Due to the exponential scaling of the complexity of structure search (Eq.1.1.1), the advantages of USPEX increase exponentially with system size. For instance, 2 out of 3 structures of SiH\(_4\) predicted by random sampling to be stable 7, turned out to be unstable 8; and similarly random sampling predictions were shown 9 to be incorrect for nitrogen 10 and for SnH4 (compare predictions 11 of USPEX and of random sampling 12).

For larger systems, random sampling tends to produce almost exclusively disordered structures with nearly identical energies, which decreases the success rate to practically zero, as shown in the example of MgSiO\(_3\) post-perovskite with 40 atoms/supercell — random sampling fails to find the correct structure even after 120,000 relaxations, whereas USPEX finds it after several hundred relaxations (Fig. 1.1.4).

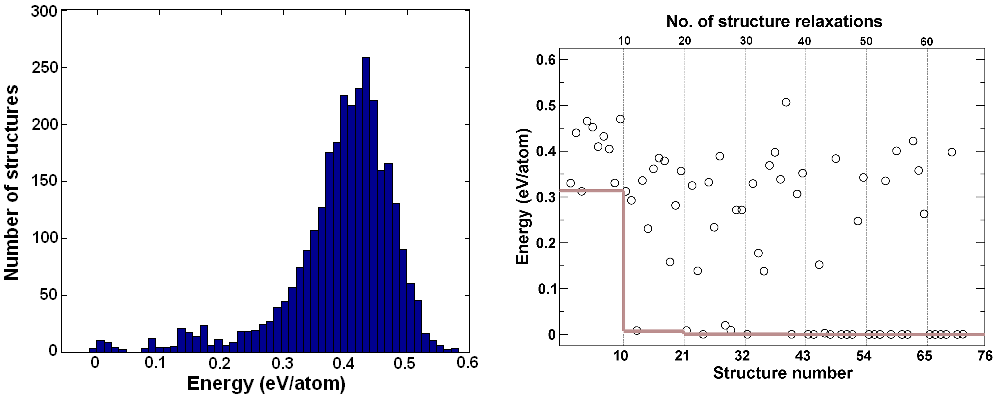
_images/Structure_prediction_for_GaAs_ab.png

Fig. 1.1.3 a) Energy distribution for relaxed random structures, b) progress of an evolutionary simulation (thin vertical lines show generations of structures, and the grey line shows the lowest energy as a function of generation). All energies are relative to the ground-state structure. The evolutionary simulation used 10 structures per generation. In addition, the lowest-energy structure of the previous generation survived into the next generation.

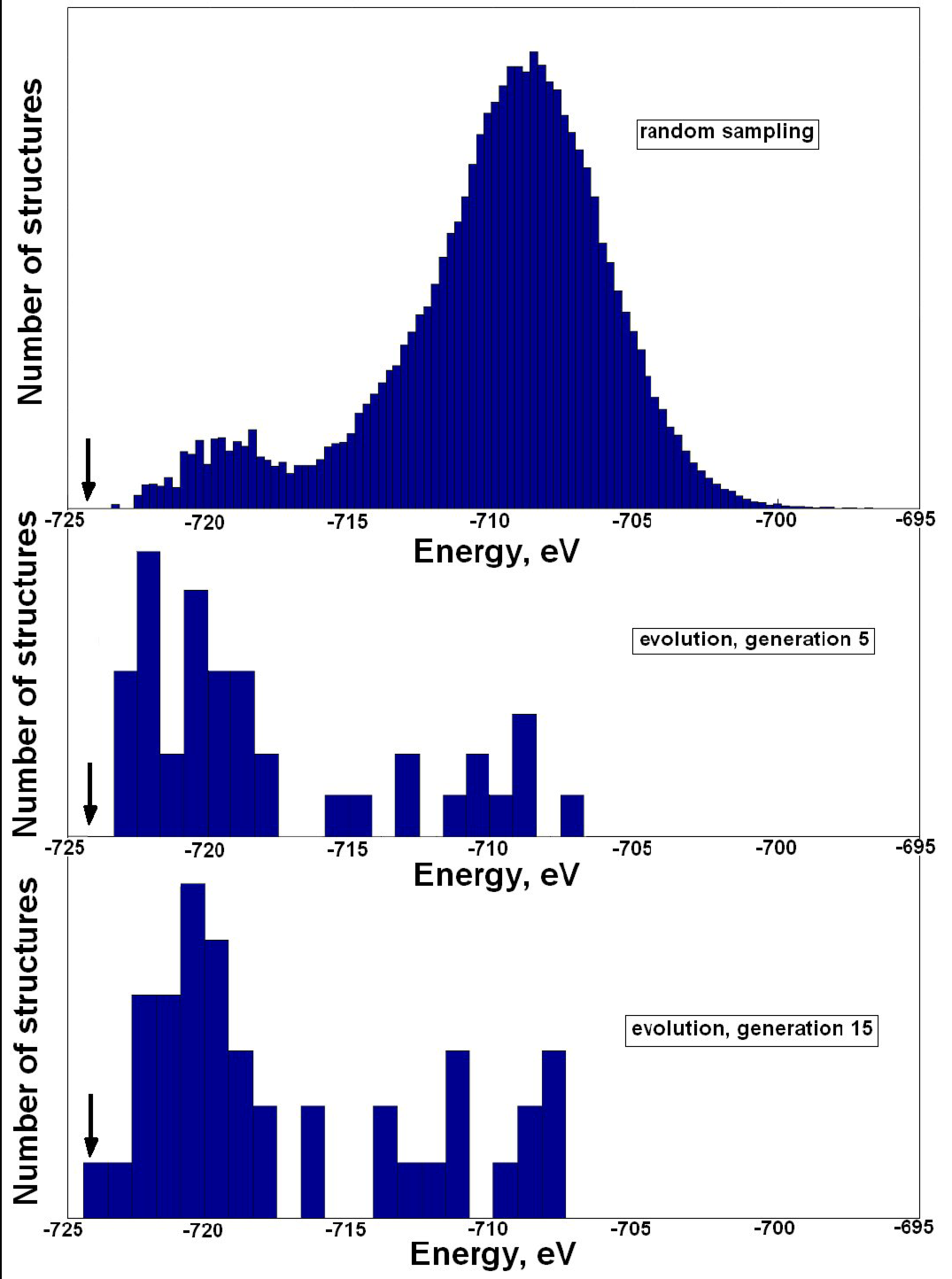
_images/Sampling_of_the_energy_surface.png

Fig. 1.1.4 Sampling of the energy surface: comparison of random sampling and USPEX for a 40-atom cell of MgSiO\(_3\) with cell parameters of post-perovskite. Energies of locally optimized structures are shown. For random sampling, \(1.2\times 10^{5}\) structures were generated (none of which corresponded to the ground state). For USPEX search, each generation included 40 structures and the ground-state structure was found within 15 generations. The energy of the ground-state structure is indicated by the arrow. This picture shows that “learning” incorporated in evolutionary search drives the simulation towards lower-energy structures.

Random sampling runs can easily be performed with USPEX — but we see this useful mostly for testing. Likewise, the Particle Swarm Optimization (PSO) algorithm for cluster and crystal structure prediction (first developed for predicting structures of clusters by A.I.Boldyrev 13) has been revamped and implemented on the basis of USPEX with minor programming work as a corrected PSO (corPSO) algorithm, which outperformed previous versions of PSO. Still, any version of PSO is rather weak and we see the PSO approach suitable mostly for testing purposes, if anyone wants to try. A very powerful new method, complementary to our evolutionary algorithm, is evolutionary metadynamics 14, a hybrid of Martoňák’s metadynamics and the our evolutionary approach. This method is powerful for global optimization and for harvesting low-energy metastable structures, and even for finding possible phase transition pathways. For detailed investigations of phase transition mechanisms, additional methods are implemented: variable-cell NEB method 15 and transition path method 16 in the version 17.

1.2. Features of USPEX

  • Prediction of the stable and metastable structures knowing only the chemical composition. Simultaneous searches for stable compositions and structures are also possible.

  • Incorporation of partial structural information is possible:

    • constraining search to fixed experimental cell parameters, or fixed cell shape, or fixed cell volume (Section 5.6.2);

    • starting structure search from known or hypothetical structures (Section 5.6.14);

    • assembling crystal structures from predefined molecules (Section 5.10).

  • Efficient constraint techniques, which eliminate unphysical and redundant regions of the search space. Cell reduction technique (Oganov & Glass, 2008 18).

  • Niching using fingerprint functions (Oganov & Valle, 2009 19; Lyakhov, Oganov, Valle, 2010 20). Section 5.6.5 for details.

  • Initialization using fully random approach, or using space groups and cell splitting techniques (Lyakhov, Oganov, Valle, 2010 20). Use of powerful topological structure generator (Bushlanov, Blatov, Oganov, 2018 21).

  • Prediction of the structure of nanoparticles and surface reconstructions.

  • Restart functionality.

  • USPEX is interfaced with VASP, GULP, LAMMPS, ABINIT, Quantum Espresso, FHIaims, MOPAC codes. See full list of supported codes in Subsection Section 2.5.

  • Submission of jobs from local workstation to remote clusters and supercomputers is possible.

1.3. Key USPEX papers

  1. Oganov A.R., Glass C.W. (2006). Crystal structure prediction using evolutionary algorithms: principles and applications. J. Chem. Phys., 124, 244704.

  2. Oganov A.R., Stokes H., Valle M. (2011). How evolutionary crystal structure prediction works — and why. Acc. Chem. Res., 44, 227–237.

  3. Lyakhov A.O., Oganov A.R., Stokes H., Zhu Q. (2013). New developments in evolutionary structure prediction algorithm USPEX. Comp. Phys. Comm., 184, 1172–1182.

  4. Zhu Q., Oganov A.R., Glass C.W., Stokes H. (2012). Constrained evolutionary algorithm for structure prediction of molecular crystals: methodology and applications. Acta Cryst. B, 68, 215–226.

  5. Zhu Q., Li L., Oganov A.R., Allen P.B. (2013). Evolutionary method for predicting surface reconstructions with variable stoichiometry. Phys. Rev. B, 87, 195317.

  6. Zhu, Q., Sharma V., Oganov A.R., Ramprasad R. (2014). Predicting polymeric crystal structures by evolutionary algorithms. J. Chem. Phys., 141, 154102.

  7. Lyakhov A.O., Oganov A.R., Valle M. (2010). Crystal structure prediction using evolutionary approach. In: Modern methods of crystal structure prediction (ed: A.R. Oganov), Berlin: Wiley-VCH.

  8. Oganov A.R., Ma Y., Lyakhov A.O., Valle M., Gatti C. (2010). Evolutionary crystal structure prediction as a method for the discovery of minerals and materials. Rev. Mineral. Geochem., 71, 271–298.

  9. Duan, D., Liu, Y., Tian, F., Li, D., Huang, X., Zhao, Z., Yu, H., Liu, B., Tian, W., Cui, T. (2014). Pressure-induced metallization of dense (H\(_2\)S)\(_2\)H\(_2\) with high-\(T_c\) superconductivity. Sci. Rep., 4, 6968.

  10. Bushlanov P.V., Blatov V.A., Oganov A.R. (2019). Topology-based crystal structure generator. Comp. Phys. Comm., DOI: 10.1016/j.cpc.2018.09.016.

  11. Lepeshkin S.V., Baturin V.S., Uspenskii Yu.A., Oganov A.R. (2019). Method for simultaneous prediction of atomic structure of nanoclusters in a wide area of compositions. J. Phys. Chem. Lett. 10, 102-106.

  12. Allahyari Z., Oganov A.R. (2018). Multi-objective optimization as a tool for materials design. In:.Handbook of Materials Modeling (ed. W. Andreoni, S. Yip). Volume 2 Applications: Current and Emerging Materials. Springer Verlag.

  13. Allahyari Z., Oganov A.R. (2020). Coevolutionary search for optimal materials in the space of all possible compounds. npj Computational Materials volume 6, Article number: 55.

  14. Liu X., Niu H., Oganov A.R. (2021). COPEX: co-evolutionary crystal structure prediction algorithm for complex systems. npj Comp. Mater. 7, 199

1.4. Version history